Topological Sort

Time Complexity: O(V+E)

DFS

DFS-based algorithm from geeksforgeeks

BFS

Kahn's algorithm

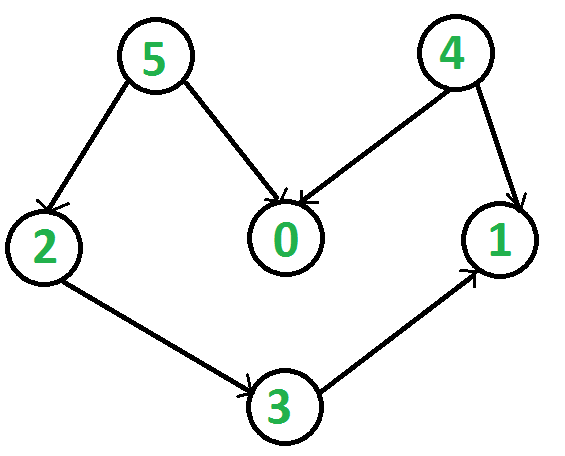
Departure time of vertex

Topological Sort of a graph using departure time of vertex

What is Arrival Time & Departure Time of Vertices in DFS?

In DFS, Arrival Time is the time at which the vertex was explored for the first time and Departure Time is the time at which we have explored all the neighbors of the vertex and we are ready to backtrack.

How to find Topological Sort of a graph using departure time?

To find Topological Sort of a graph, we run DFS starting from all unvisited vertices one by one. For any vertex, before exploring any of its neighbors, we note the arrival time of that vertex and after exploring all the neighbors of the vertex, we note its departure time. Please note only departure time is needed to find Topological Sort of a graph, so we can skip arrival time of vertex. Finally, after we have visited all the vertices of the graph, we print the vertices in order of their decreasing departure time which is our desired Topological Order of Vertices.

// The function to do DFS() and stores departure time 
// of all vertex
void Graph::DFS(int v, vector<bool> &visited, 
                vector<int> &departure, int &time)
{
    visited[v] = true;
    // time++;    // arrival time of vertex v

    for(int i : adj[v])
        if(!visited[i])
            DFS(i, visited, departure, time);

    // set departure time of vertex v
    departure[++time] = v;
}

// The function to do Topological Sort. It uses DFS().
void Graph::topologicalSort()
{
    // vector to store departure time of vertex.
    vector<int> departure(V, -1);

    // Mark all the vertices as not visited
    vector<bool> visited(V, false);
    int time = -1;

    // perform DFS on all unvisited vertices
    for(int i = 0; i < V; i++)
        if(!visited[i])
            DFS(i, visited, departure, time);

    // Print vertices in topological order
    for(int i = V - 1; i >= 0; i--)
        cout << departure[i] << " ";
}