548. Split Array with Equal Sum (Medium)
Given an array with n integers, you need to find if there are triplets (i, j, k) which satisfies following conditions:
- 0 < i, i + 1 < j, j + 1 < k < n - 1
- Sum of subarrays (0, i - 1), (i + 1, j - 1), (j + 1, k - 1) and (k + 1, n - 1) should be equal.
where we define that subarray (L, R) represents a slice of the original array starting from the element indexed L to the element indexed R.
Example:
Input: [1,2,1,2,1,2,1]
Output: True
Explanation:
i = 1, j = 3, k = 5.
sum(0, i - 1) = sum(0, 0) = 1
sum(i + 1, j - 1) = sum(2, 2) = 1
sum(j + 1, k - 1) = sum(4, 4) = 1
sum(k + 1, n - 1) = sum(6, 6) = 1
Note:
- $$1 \le n \le 2000$$.
- Elements in the given array will be in range [-1,000,000, 1,000,000].
Summary
Given an array with n integers, you need to find if there are triplets (i, j, k) which satisfies following conditions:
0 < i, i + 1 < j, j + 1 < k < n - 1
sum of subarrays (0, i - 1), (i + 1, j - 1), (j + 1, k - 1) and (k + 1, n - 1) should be equal.
where subarray (L, R) represents a slice of the original array starting from the L-th element to the R-th.
Solution: Skip 0s
version 1: 22ms
class Solution {
public:
bool splitArray(vector<int>& nums) {
if (nums.size() < 7) return false;
int n = nums.size();
vector<int> sum(n,0); sum[0] = nums[0];
for (int i = 1; i < n; ++i) sum[i] = sum[i-1]+nums[i];
int s1 = 0, s2 = 0, s3 = 0, s4 = 0;
for (int i = 1; i < n-1; ++i) {
if (i != 1 && nums[i] == 0 && nums[i] == nums[i-1]) continue;
s1 = sum[i-1];
for (int j = i+2; j < n-1; ++j) {
if (j != i+2 && nums[j] == 0 && nums[j] == nums[j-1]) continue;
s2 = sum[j-1]-sum[i];
if (s1 != s2) continue;
for (int k = j+2; k < n-1; ++k) {
if (k != j+2 && nums[k] == 0 && nums[k] == nums[k-1]) continue;
s3 = sum[k-1]-sum[j];
if (s2 != s3) continue;
s4 = sum[n-1]-sum[k];
if (s3 != s4) continue;
return true;
}
}
}
return false;
}
};
version 2: 15ms
class Solution {
public:
bool splitArray(vector<int>& nums) {
int prev = 0;
vector<int> sum;
for (int i = 0; i < nums.size(); ++i) {
if (nums[i] == 0 && i > 0 && nums[i-1] == 0) continue; // skip extra 0s to accelerate
prev += nums[i];
sum.push_back(prev);
}
int n = sum.size();
for (int i = 1; i < n; ++i) {
int sum1 = sum[i-1];
for (int j = i+2; j < n-3; ++j) {
int sum2 = sum[j-1]-sum[i];
if (sum1 != sum2) continue;
for (int k = j+2; k < n-1; ++k) {
int sum3 = sum[k-1]-sum[j];
int sum4 = sum[n-1]-sum[k];
if (sum2 == sum3 && sum3 == sum4) return true;
}
}
}
return false;
}
};
Solution
Approach #1 Brute Force [Time Limit Exceeded]
Algorithm
Before we start looking at any of the approaches for solving this problem, firstly we need to look at the limits imposed onii,jjandkkby the given set of constraints. The figure below shows the maximum and minimum values thatii,jjandkkcan assume.
Thus, the limits based on the length of the array nn can now be rewritten as:
$$1≤i≤n−6$$
$$i+2≤j≤n−4$$
$$j+2≤k≤n−2$$
Having discussed the limits imposed on the cuts $$i$$, $$j$$, $$k$$ that we will apply on the given array $$nums$$, let's look at the first solution that comes to our mind.
We simply traverse over all the elements of the array. We consider all the possible subarrays taking care of the constraints imposed on the cuts, and check if any such cuts exist which satisfy the given equal sum quadruples criteria.
Java
public class Solution {
public int sum(int[] nums, int l, int r) {
int summ = 0;
for (int i = l; i < r; i++)
summ += nums[i];
return summ;
}
public boolean splitArray(int[] nums) {
if (nums.length < 7)
return false;
for (int i = 1; i < nums.length - 5; i++) {
int sum1 = sum(nums, 0, i);
for (int j = i + 2; j < nums.length - 3; j++) {
int sum2 = sum(nums, i + 1, j);
for (int k = j + 2; k < nums.length - 1; k++) {
int sum3 = sum(nums, j + 1, k);
int sum4 = sum(nums, k + 1, nums.length);
if (sum1 == sum2 && sum3 == sum4 && sum2 == sum4)
return true;
}
}
}
return false;
}
}
Complexity Analysis
- Time complexity: $$O(n^4)$$. Four for loops inside each other each with a worst case run of length nn.
- Space complexity: $$O(1)$$. Constant Space required.
Approach #2 Cumulative Sum [Time Limit Exceeded]
Algorithm
In the brute force approach, we traversed over the subarrays for every triplet of cuts considered. Rather than doing this, we can save some calculation effort if we make use of a cumulative sum array $$sum$$, where $$sum[i]$$ stores the cumulative sum of the array $$nums$$ upto the $$i^{th}$$ element. Thus, now in order to find the $$sum(subarray(i:j)$$, we can simply use $$sum[j]-sum[i]$$. Rest of the process remains the same.
c++
class Solution {
public:
bool splitArray(vector<int>& nums) {
if (nums.size() < 7) return false;
int n = nums.size();
vector<int> sum(n); sum[0] = nums[0];
for (int i = 1; i < n; ++i) {
sum[i] = sum[i-1]+nums[i];
}
for (int i = 1; i < n-5; ++i) {
int sum1 = sum[i-1];
for (int j = i+2; j < n-3; ++j) {
int sum2 = sum[j-1]-sum[i];
for (int k = j+2; k < n-1; ++k) {
int sum3 = sum[k-1]-sum[j];
int sum4 = sum[n-1]-sum[k];
if (sum1 == sum2 && sum2 == sum3 && sum3 == sum4) return true;
}
}
}
return false;
}
};
Complexity Analysis
- Time complexity: $$O(n^3)$$. Three for loops are there, one within the other.
- Space complexity: $$O(n)$$. $$sum$$ array of size $$n$$ is used for storing cumulative sum.
Approach #3 Slightly Better Approach [Time Limit Exceeded]
Algorithm
We can improve the previous implementation to some extent if we stop checking for further quadruples if the first and second parts formed till now don't have equal sums. This idea is used in the current implementation.
c++
class Solution {
public:
bool splitArray(vector<int>& nums) {
if (nums.size() < 7) return false;
int n = nums.size();
vector<int> sum(n); sum[0] = nums[0];
for (int i = 1; i < n; ++i) {
sum[i] = sum[i-1]+nums[i];
}
for (int i = 1; i < n-5; ++i) {
int sum1 = sum[i-1];
for (int j = i+2; j < n-3; ++j) {
int sum2 = sum[j-1]-sum[i];
if (sum1 != sum2) continue;
for (int k = j+2; k < n-1; ++k) {
int sum3 = sum[k-1]-sum[j];
int sum4 = sum[n-1]-sum[k];
if (sum2 == sum3 && sum3 == sum4) return true;
}
}
}
return false;
}
};
Complexity Analysis
- Time complexity: $$O(n^3)$$. Three loops are there.
- Space complexity: $$O(n)$$. $$sum$$ array of size $$n$$ is used for storing the cumulative sum.
Approach #4 Using HashMap [Time limit Exceeded]
Algorithm
In this approach, we create a data structure called $$map$$ which is simply a HashMap, with data arranged in the format:
$$csum(i)$$ represents the cumulative sum in the given array $$nums$$ upto the $$i^{th}$$ index.
Once we create this $$map$$, the solutions gets simplified a lot. Consider only the first two cuts formed by $$i$$ and $$j$$. Then, the cumulative sum upto the $$(j-1)^{th}$$ index will be given by: $$csum(j-1)=sum(first quadruple) + nums[i] + sum(second quadruple)$$. Now, if we want the first two quadruples to have the same sum, the same cumulative sum can be rewritten as: $$csum'(j-1) = csum(i-1) + nums[i] + csum(i-1) = 2csum(i-1) + nums[i]$$.
Thus, we traverse over the given array, changing the value of the index $$i$$ forming the first cut, and look if the $$map$$ formed initially contains a cumulative sum equal to $$csum'(j-1)$$. If $$map$$ contains such a cumulative sum, we consider every possible index $$j$$ satisfying the given constraints and look for the equalities of the first cumulative sum with the third and the fourth quadruples.
Following the similar lines as the discussion above, the cumulative sum upto the third cut by $$k^{th}$$ index is given by $$csum(k-1) = sum(first quadruple) + nums[i] + sum(second quadruple) + nums[j] + sum(third quadruple)$$. For equality of sum, the condition becomes: $$csum'(k-1) = 3csum(i-1) + nums[i] + nums[j]$$. Similarly, the cumulative sum upto the last index becomes: $$csum(end) = sum(first quadruple) + nums[i] + sum(second quadruple) + nums[j] + sum(third quadruple) + nums[k] + sum(fourth quadruple)$$. Again, for equality, the condition becomes $$csum'(end) = 4csum(i-1) + nums[i] + nums[j] + nums[k]$$.
For every cut chosen, we look if the required cumulative sum exists in $$map$$. Thus, we need not calculate sums again and again or traverse over the array for all the triplets $$(i, j, k)$$ possible. Rather, now, we directly know, what cumulative sum to look for in the $$map$$, which reduces a lot of computations.
c++
class Solution {
public:
bool splitArray(vector<int>& nums) {
unordered_map<int, vector<int>> m;
int sum = 0, tot = 0, n = nums.size();
for (int i = 0; i < n; ++i) {
sum += nums[i];
m[sum].push_back(i);
}
tot = sum;
sum = nums[0];
for (int i = 1; i < n-5; ++i) {
if (m.find(2*sum+nums[i]) != m.end()) {
for (int j: m[2*sum+nums[i]]) {
++j;
if (j > i+1 && j < n-3 && m.find(3*sum+nums[i]+nums[j]) != m.end()) {
for (int k: m[3*sum+nums[i]+nums[j]]) {
++k;
if (k > j+1 && k < n-1 && 4*sum+nums[i]+nums[j]+nums[k] == tot)
return true;
}
}
}
}
sum += nums[i];
}
return false;
}
};
Complexity Analysis
- Time complexity: $$ O(n^3)$$. Three nested loops are there and every loop runs $$n$$ times in the worst case. Consider the worstcase [0,0,0....,1,1,1,1,1,1,1].
- Space complexity: $$O(n)$$. HashMap size can go upto $$n$$.
Approach #5 Using Cumulative Sum and HashSet [Accepted]
Algorithm
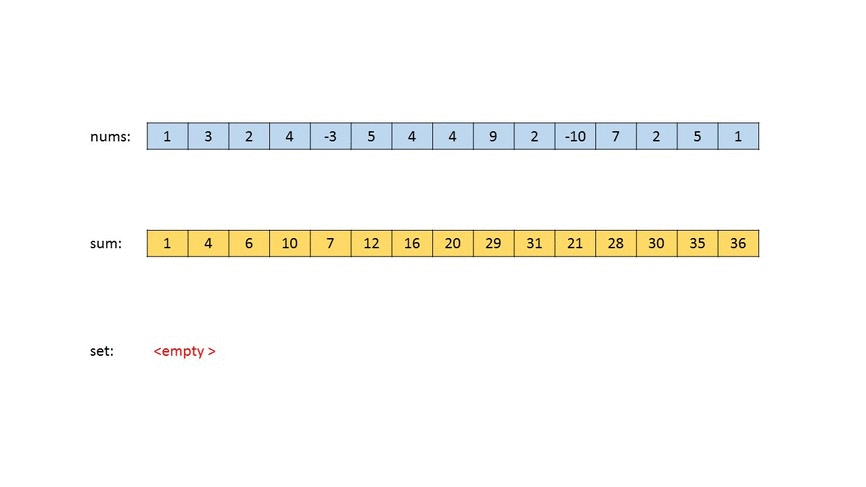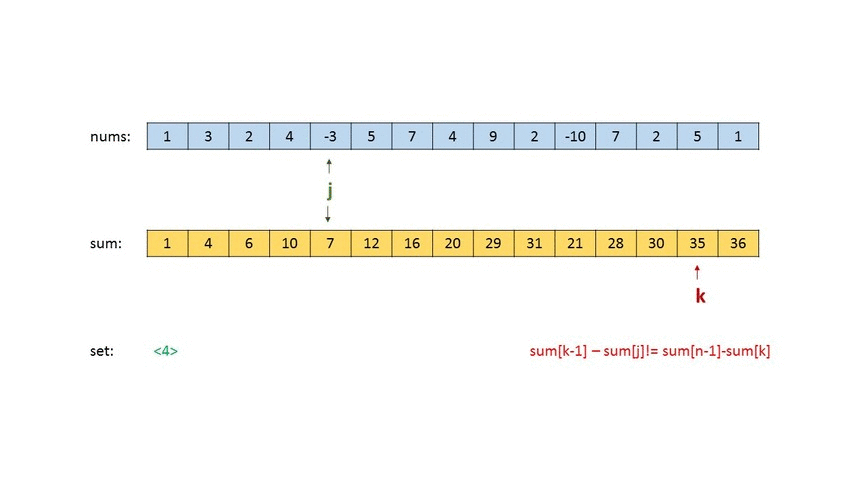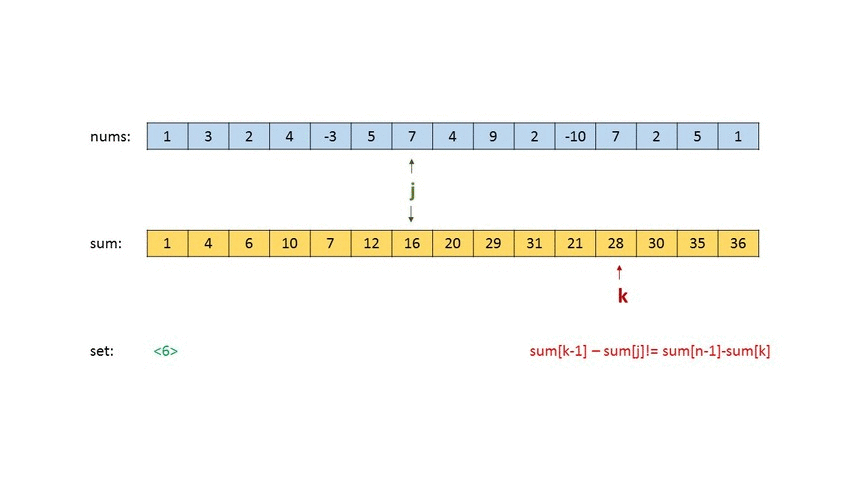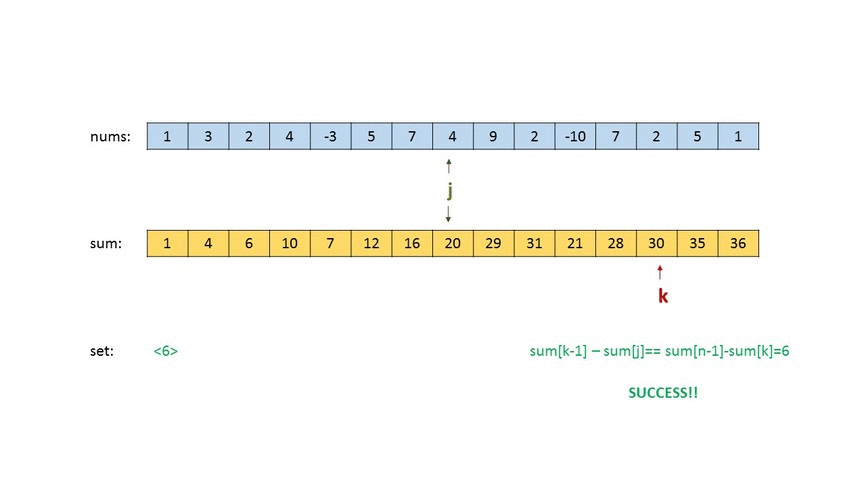
In this approach, firstly we form a cumulative sum array $$sum$$, where $$sum[i]$$ stores the cumulative sum of the array $$nums$$ upto the $$i^{th}$$ index. Then, we start by traversing over the possible positions for the middle cut formed by $$j$$. For every $$j$$, firstly, we find all the left cut's positions,$$i$$, that lead to equalizing the sum of the first and the second quarter (i.e. $$sum[i−1]=sum[j−1]−sum[i]$$) and store such sums in the $$set$$(a new HashSet is formed for every $$j$$ chosen). Thus, the presence of a sum in $$set$$ implies that such a sum is possible for having equal sum of the first and second quarter for the current position of the middle cut ($$j$$).
Then, we go for the right cut and find the position of the right cut that leads to equal sum of the third and the fourth quarter($$sum[n-1]-sum[k]=sum[k-1] - sum[j]$$), for the same middle cut as chosen earlier. We also, look if the same sum exists in the $$set$$. If so, such a triplet $$(i, j, k)$$ exists which satisfies the required criteria, otherwise not.
Look at the animation below for a visual representation of the process:
c++ 189ms
class Solution {
public:
bool splitArray(vector<int>& nums) {
if (nums.size() < 7) return false;
int n = nums.size();
vector<int> sum(n); sum[0] = nums[0];
for (int i = 1; i < n; ++i) sum[i] = sum[i-1]+nums[i];
for (int j = 3; j < n-3; ++j) {
unordered_set<int> s;
for (int i = 1; i < j-1; ++i) {
if (sum[i-1] == sum[j-1]-sum[i]) s.insert(sum[i-1]);
}
for (int k = j+2; k < n-1; ++k) {
if (sum[n-1]-sum[k] == sum[k-1]-sum[j] && s.count(sum[n-1]-sum[k])) return true;
}
}
return false;
}
};
Complexity Analysis
- Time complexity: $$O(n^2)$$. One outer loop and two inner loops are used.
- Space complexity: $$O(n)$$. HashSet size can go upto $$n$$.