208. Implement Trie (Prefix Tree) (Medium)

Implement a trie with insert, search, and startsWith methods.

Note: You may assume that all inputs are consist of lowercase letters a-z.

Solution: Trie

这道题让我们实现一个重要但又有些复杂的数据结构-字典树， 又称前缀树或单词查找树，详细介绍可以参见网友董的博客，例如，一个保存了8个键的trie结构，"A", "to", "tea", "ted", "ten", "i", "in", and "inn".如下图所示：

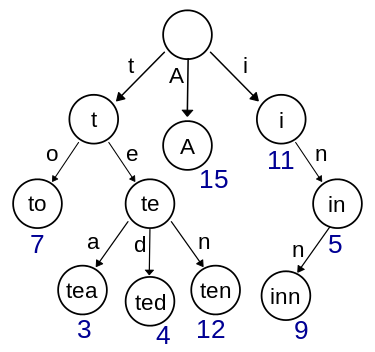
字典树主要有如下三点性质：

1. 根节点不包含字符，除根节点以外每个节点只包含一个字符。
2. 从根节点到某一个节点，路径上经过的字符连接起来，为该节点对应的字符串。
3. 每个节点的所有子节点包含的字符串不相同。

字母树的插入（Insert）、删除（ Delete）和查找（Find）都非常简单，用一个一重循环即可，即第i 次循环找到前i 个字母所对应的子树，然后进行相应的操作。实现这棵字母树，我们用最常见的数组保存（静态开辟内存）即可，当然也可以开动态的指针类型（动态开辟内存）。至于结点对儿子的指向，一般有三种方法：

1. 对每个结点开一个字母集大小的数组，对应的下标是儿子所表示的字母，内容则是这个儿子对应在大数组上的位置，即标号；
2. 对每个结点挂一个链表，按一定顺序记录每个儿子是谁；
3. 使用左儿子右兄弟表示法记录这棵树。

三种方法，各有特点。第一种易实现，但实际的空间要求较大；第二种，较易实现，空间要求相对较小，但比较费时；第三种，空间要求最小，但相对费时且不易写。

我们先来看第一种实现方法，这种方法实现起来简单直观，字母的字典树每个节点要定义一个大小为26的子节点指针数组，然后用一个标志符用来记录到当前位置为止是否为一个词，初始化的时候讲26个子节点都赋为空。那么insert操作只需要对于要插入的字符串的每一个字符算出其的位置，然后找是否存在这个子节点，若不存在则新建一个，然后再查找下一个。查找词和找前缀操作跟insert操作都很类似，不同点在于若不存在子节点，则返回false。查找次最后还要看标识位，而找前缀直接返回true即可。代码如下：

class TrieNode {
public:
    // Initialize your data structure here.
    TrieNode(): isWord(false) {
        for (auto& a: child) a = NULL;
    }
    bool isWord;
    TrieNode* child[26];
};

class Trie {
public:
    Trie() {
        root = new TrieNode();
    }

    // Inserts a word into the trie.
    void insert(string word) {
        TrieNode *p = root;
        for (auto& a: word) {
            int i = a-'a';
            if (!p->child[i]) p->child[i] = new TrieNode();
            p = p->child[i];
        }
        p->isWord = true;
    }

    // Returns if the word is in the trie.
    bool search(string word) {
        TrieNode *p = root;
        for (auto& a: word) {
            int i = a-'a';
            if (!p->child[i]) return false;
            p = p->child[i];
        }
        return p->isWord;
    }

    // Returns if there is any word in the trie
    // that starts with the given prefix.
    bool startsWith(string prefix) {
        TrieNode *p = root;
        for (auto& a: prefix) {
            int i = a-'a';
            if (!p->child[i]) return false;
            p = p->child[i];
        }
        return true;
    }

private:
    TrieNode* root;
};

// Your Trie object will be instantiated and called as such:
// Trie trie;
// trie.insert("somestring");
// trie.search("key");