84. Largest Rectangle in Histogram (Hard)

Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

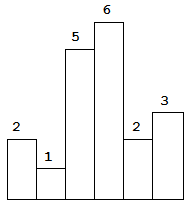
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

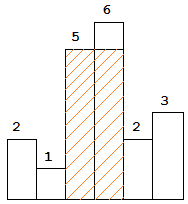
The largest rectangle is shown in the shaded area, which has area = 10 unit.

For example, Given heights = [2,1,5,6,2,3], return 10.

这里维护一个栈，用来保存递增序列，相当于上面那种方法的找局部峰值，当当前值小于栈顶值时，取出栈顶元素，然后计算当前矩形面积，然后再对比当前值和新的栈顶值大小，若还是栈顶值大，则再取出栈顶，算此时共同矩形区域面积，照此类推，可得最大矩形。代码如下：

int largestRectangleArea(vector<int>& heights) {
    int area = 0;
    stack<int> s; 
    heights.push_back(0); // ensure all heights stored in s are checked
    for (int i = 0; i < heights.size(); ++i) {
        while (!s.empty() && heights[s.top()] >= heights[i]) {
            int top = heights[s.top()]; s.pop();
            area = max(area, top*(s.empty() ? i:i-s.top()-1));
        }
        s.push(i);
    }
    return area;
}

// use vector instead of stack
int largestRectangleArea(vector<int>& heights) {
    heights.push_back(0); // ensure all heights stored in s are checked
    int area = 0, n = heights.size(), end = -1;
    vector<int> s(n); 

    for (int i = 0; i < heights.size(); ++i) {
        while (end != -1 && heights[s[end]] >= heights[i]) {
            int top = heights[s[end]]; --end;
            area = max(area, top*(end == -1 ? i:i-s[end]-1));
        }
        s[++end] = i;
    }
    return area;
}