545. Boundary of Binary Tree (Medium)

Given a binary tree, return the values of its boundary in anti-clockwise direction starting from root. Boundary includes left boundary, leaves, and right boundary in order without duplicate nodes.

Left boundary is defined as the path from root to the left-most node. Right boundary is defined as the path from root to the right-most node. If the root doesn't have left subtree or right subtree, then the root itself is left boundary or right boundary. Note this definition only applies to the input binary tree, and not applies to any subtrees.

The left-most node is defined as a leaf node you could reach when you always firstly travel to the left subtree if exists. If not, travel to the right subtree. Repeat until you reach a leaf node.

The right-most node is also defined by the same way with left and right exchanged.

Example 1

Input:
  1
   \
    2
   / \
  3   4

Ouput:
[1, 3, 4, 2]

Explanation:
The root doesn't have left subtree, so the root itself is left boundary.
The leaves are node 3 and 4.
The right boundary are node 1,2,4. Note the anti-clockwise direction means you should output reversed right boundary.
So order them in anti-clockwise without duplicates and we have [1,3,4,2].

Example 2

Input:
    ____1_____
   /          \
  2            3
 / \          / 
4   5        6   
   / \      / \
  7   8    9  10  

Ouput:
[1,2,4,7,8,9,10,6,3]

Explanation:
The left boundary are node 1,2,4. (4 is the left-most node according to definition)
The leaves are node 4,7,8,9,10.
The right boundary are node 1,3,6,10. (10 is the right-most node).
So order them in anti-clockwise without duplicate nodes we have [1,2,4,7,8,9,10,6,3].

Summary

Given a binary tree, return the values of its boundary in anti-clockwise direction starting from root. Boundary includes left boundary, leaves, and right boundary in order without duplicate nodes.

Left boundary is defined as the path from root to the left-most node. Right boundary is defined as the path from root to the right-most node. If the root doesn't have left subtree or right subtree, then the root itself is left boundary or right boundary. Note this definition only applies to the input binary tree, and not applies to any subtrees.

The left-most node is defined as a leaf node you could reach when you always firstly travel to the left subtree if exists. If not, travel to the right subtree. Repeat until you reach a leaf node.

The right-most node is also defined by the same way with left and right exchanged.

Solution

Approach #1 Simple Solution[Accepted]

Algorithm

One simple approach is to divide this problem into three subproblems- left boundary, leaves and right boundary.

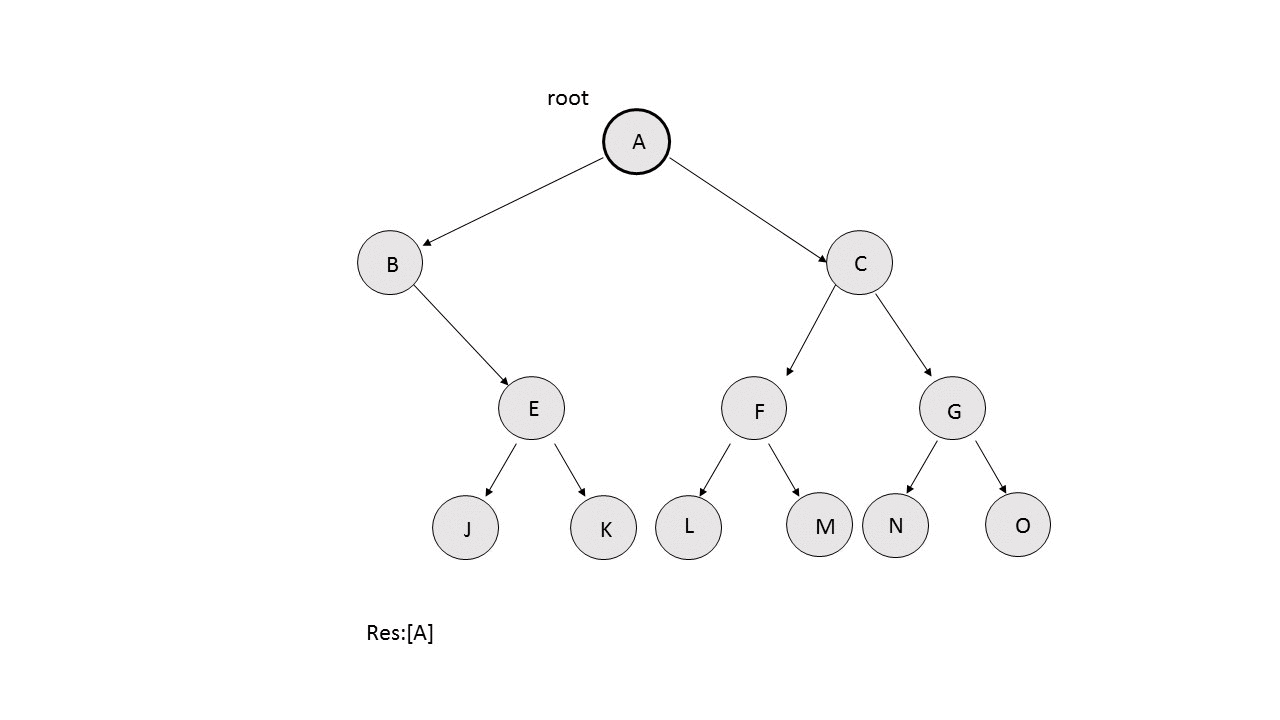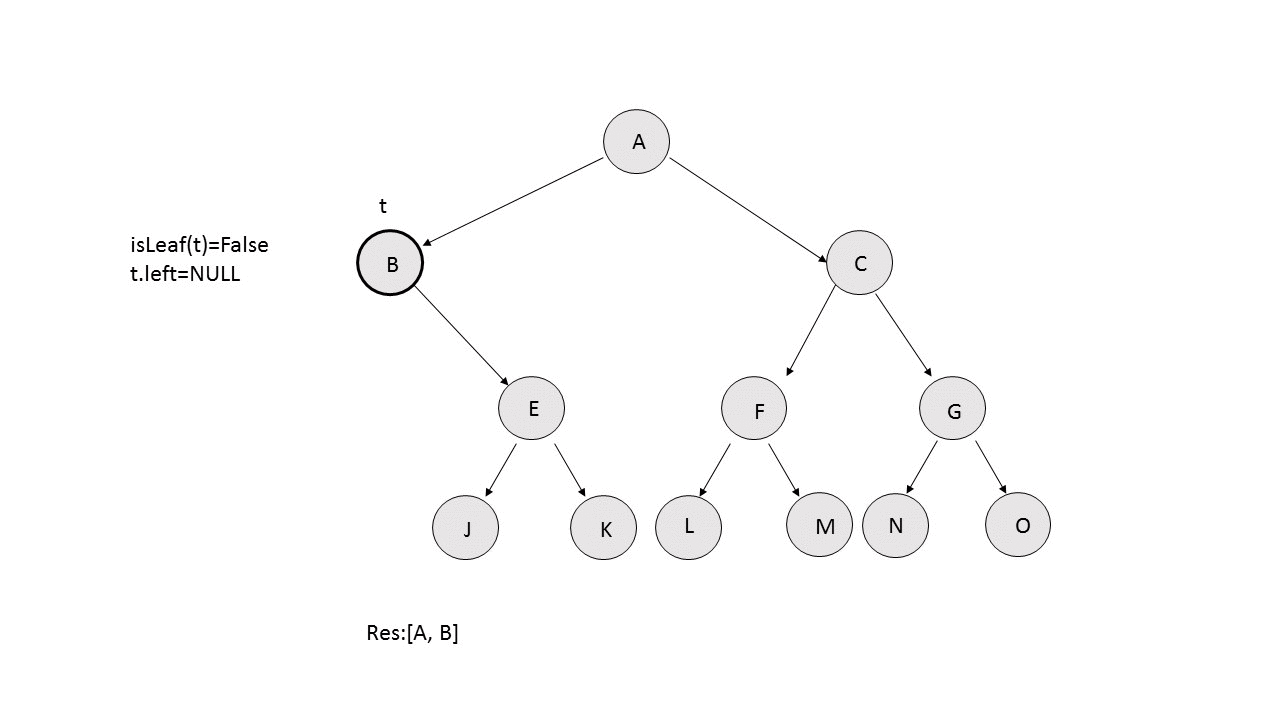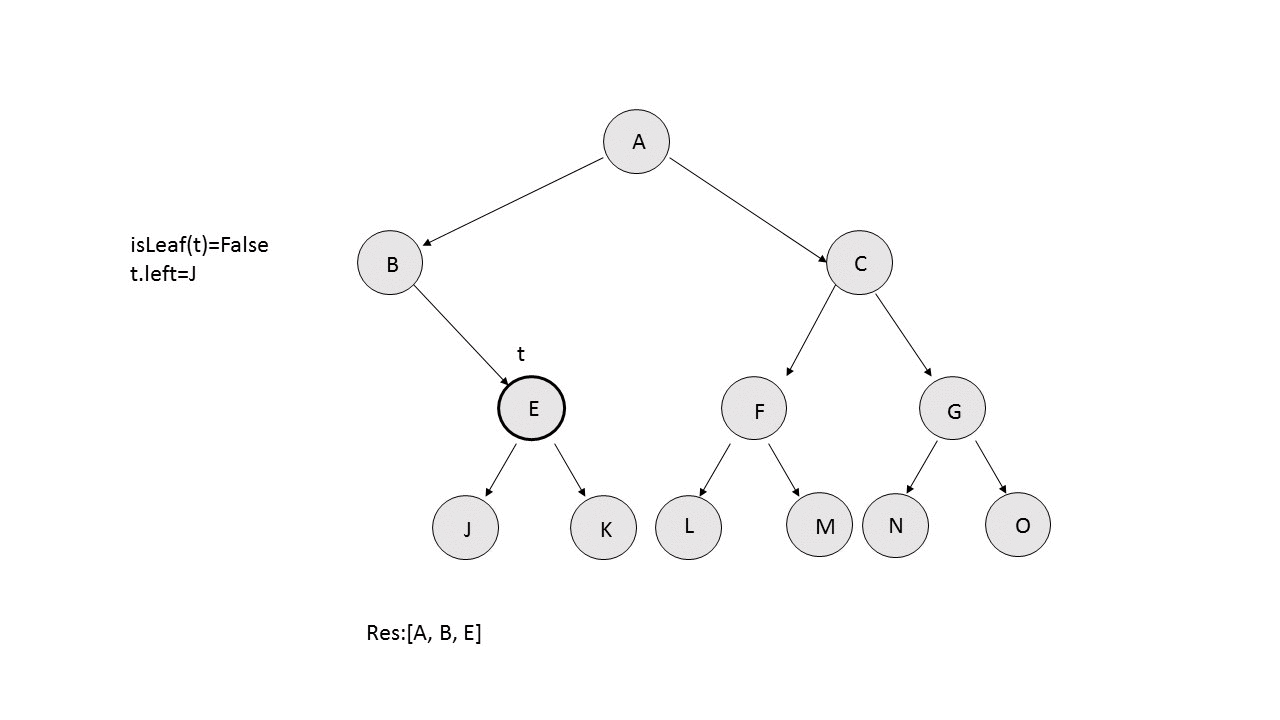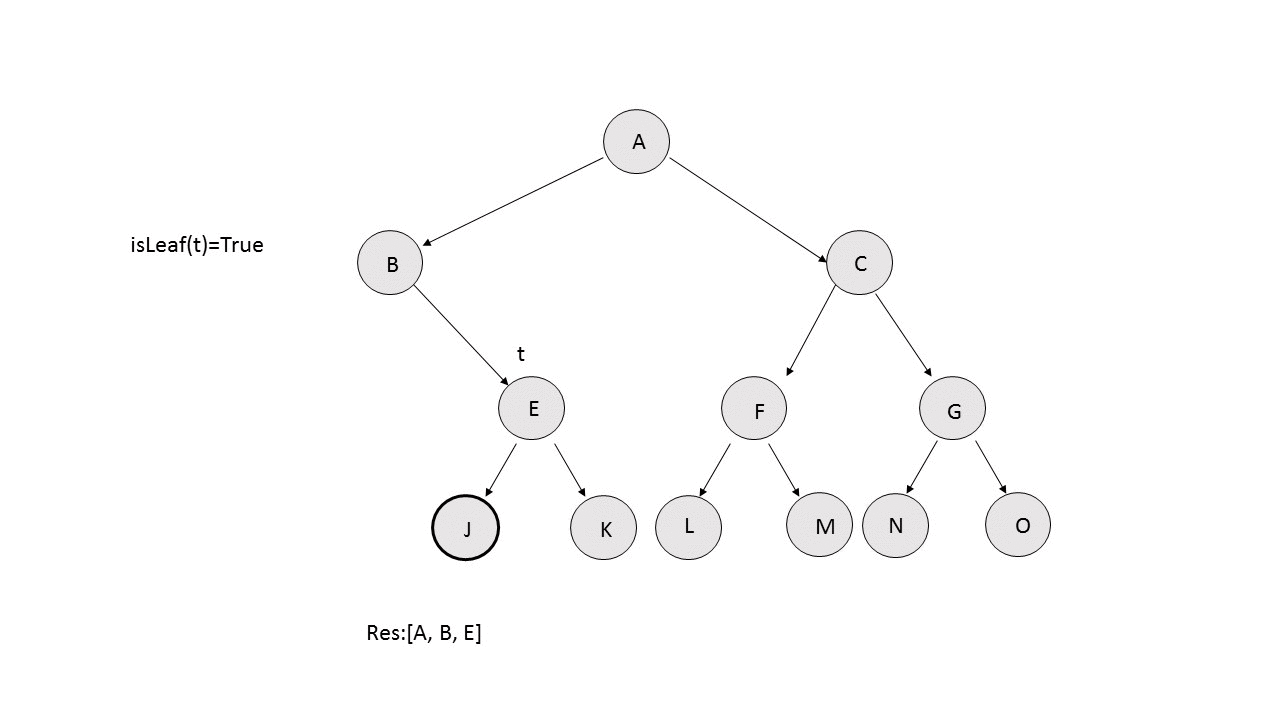
• Left Boundary: We keep on traversing the tree towards the left and keep on adding the nodes in the $$res$$ array, provided the current node isn't a leaf node. If at any point, we can't find the left child of a node, but its right child exists, we put the right child in the $$res$$ and continue the process. The following animation depicts the process.

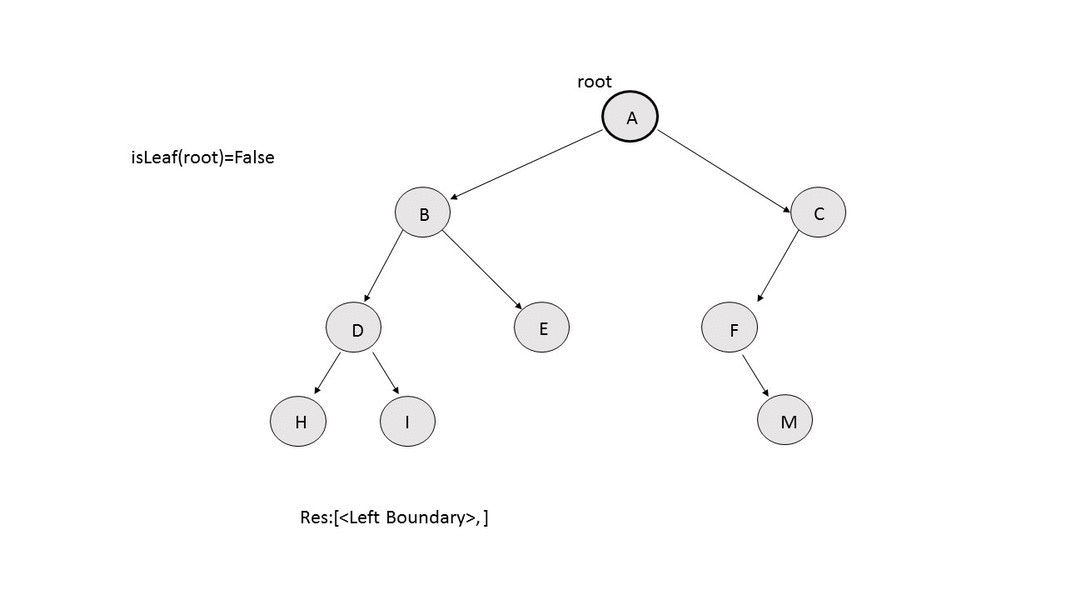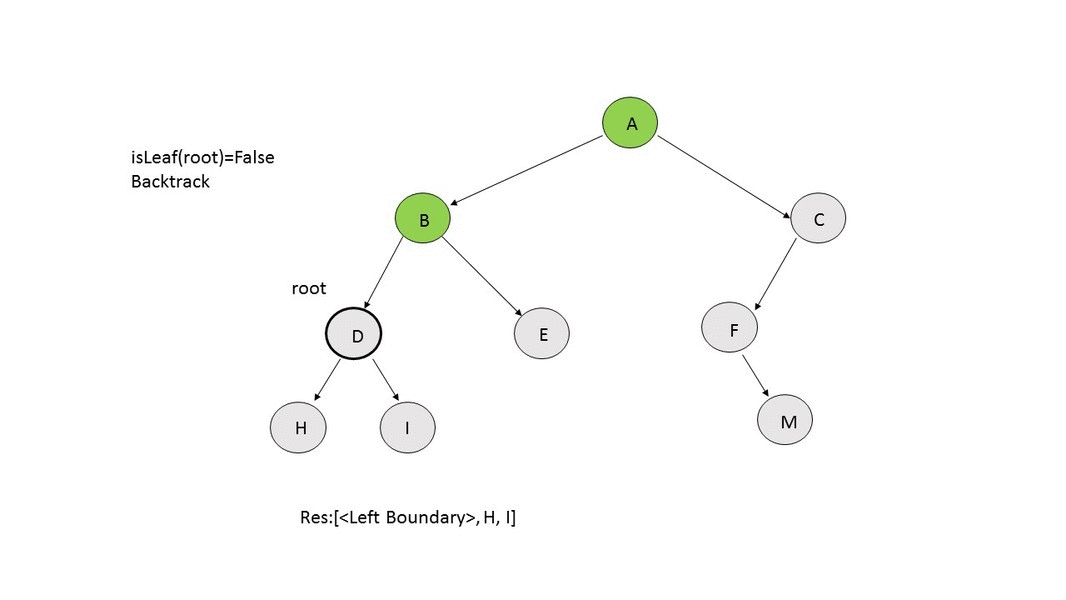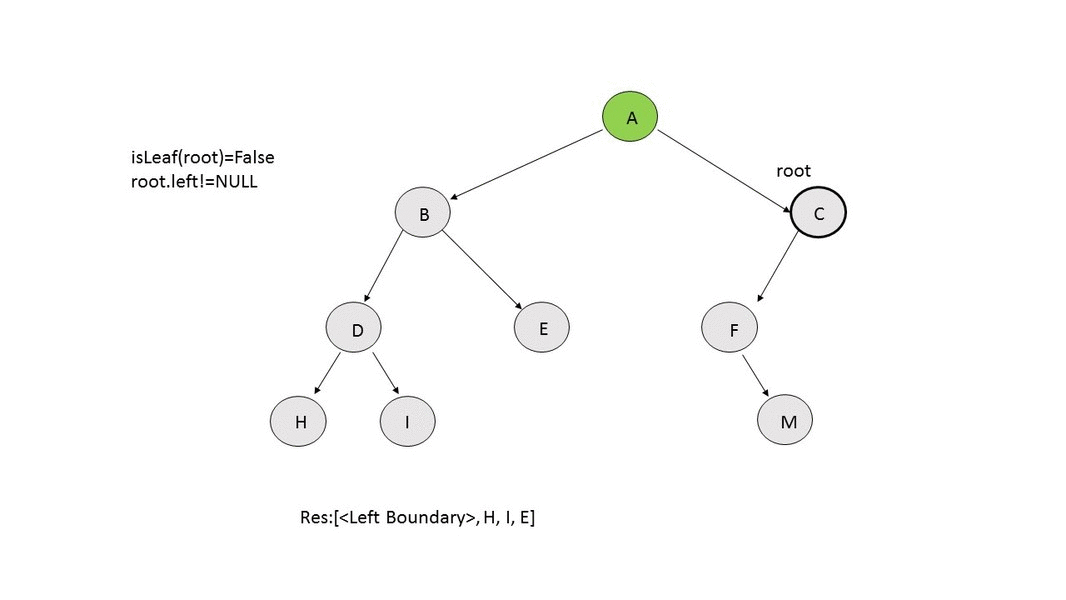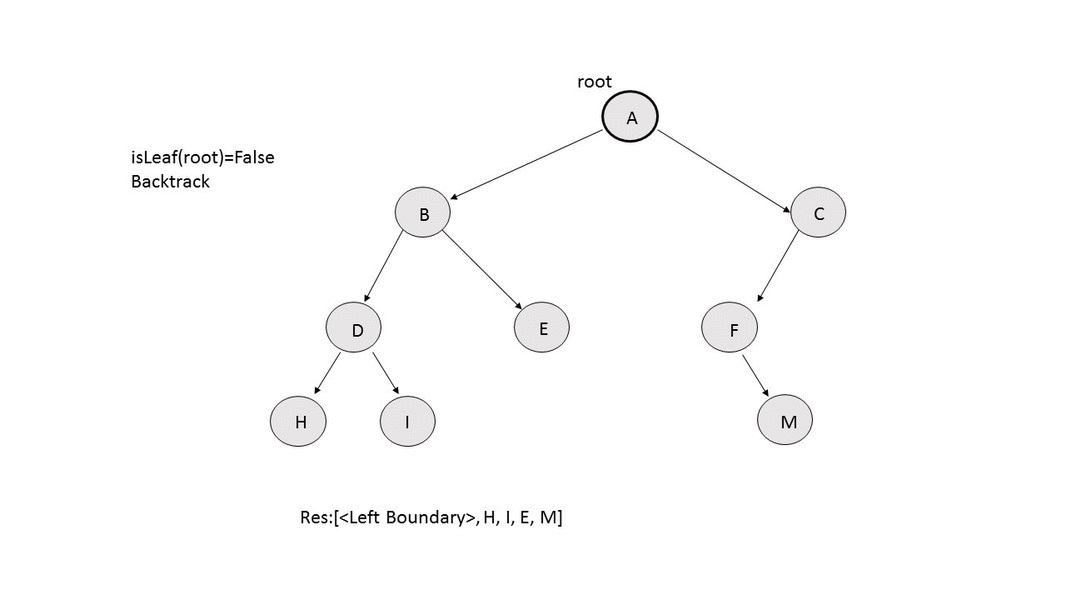
• Leaf Nodes: We make use of a recursive function addLeaves(res,root), in which we change the root node for every recursive call. If the current root node happens to be a leaf node, it is added to the $$res$$ array. Otherwise, we make the recursive call using the left child of the current node as the new root. After this, we make the recursive call using the right child of the current node as the new root. The following animation depicts the process.

• Right Boundary: We perform the same process as the left boundary. But, this time, we traverse towards the right. If the right child doesn't exist, we move towards the left child. Also, instead of putting the traversed nodes in the resres array, we push them over a stack during the traversal. After the complete traversal is done, we pop the element from over the stack and append them to the resres array. The following animation depicts the process.

/**
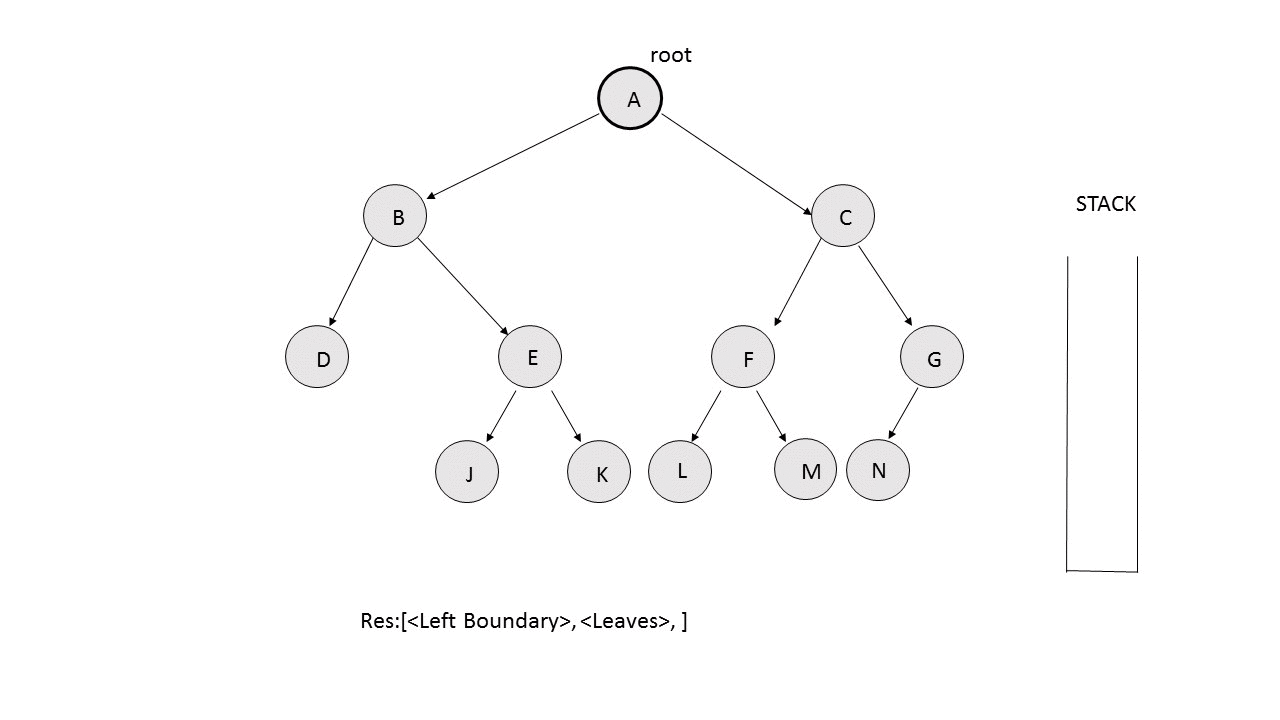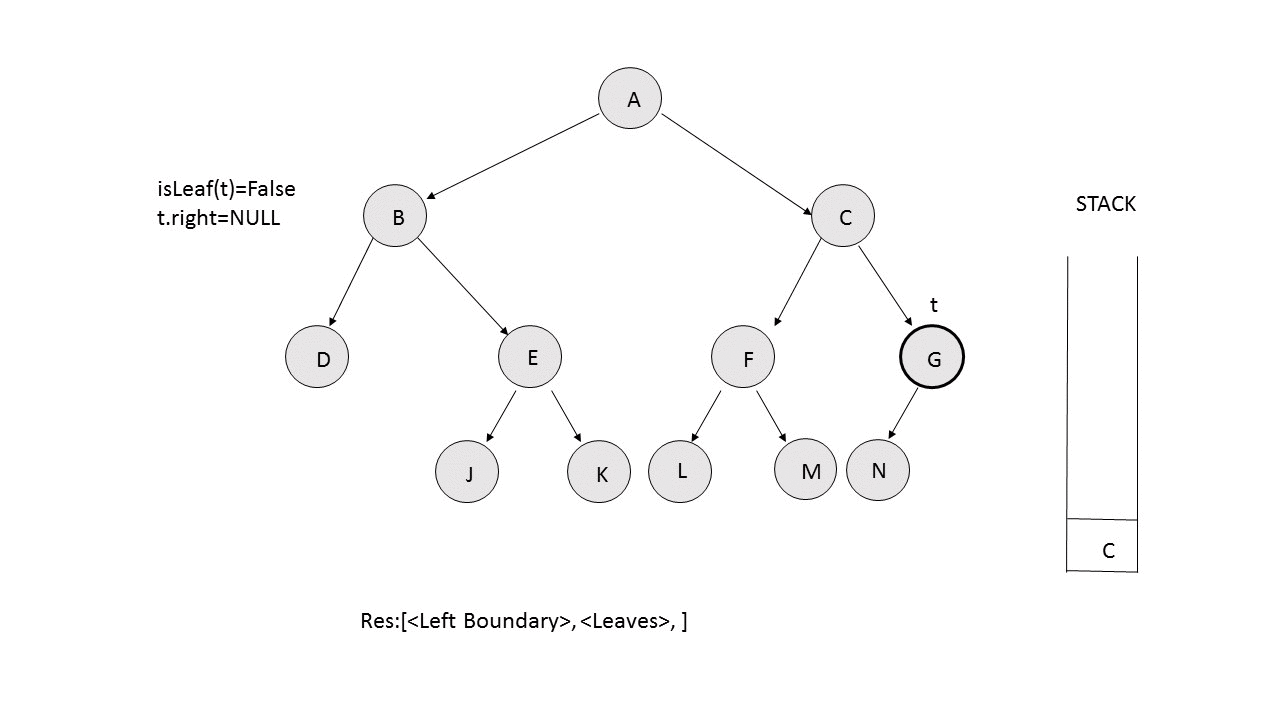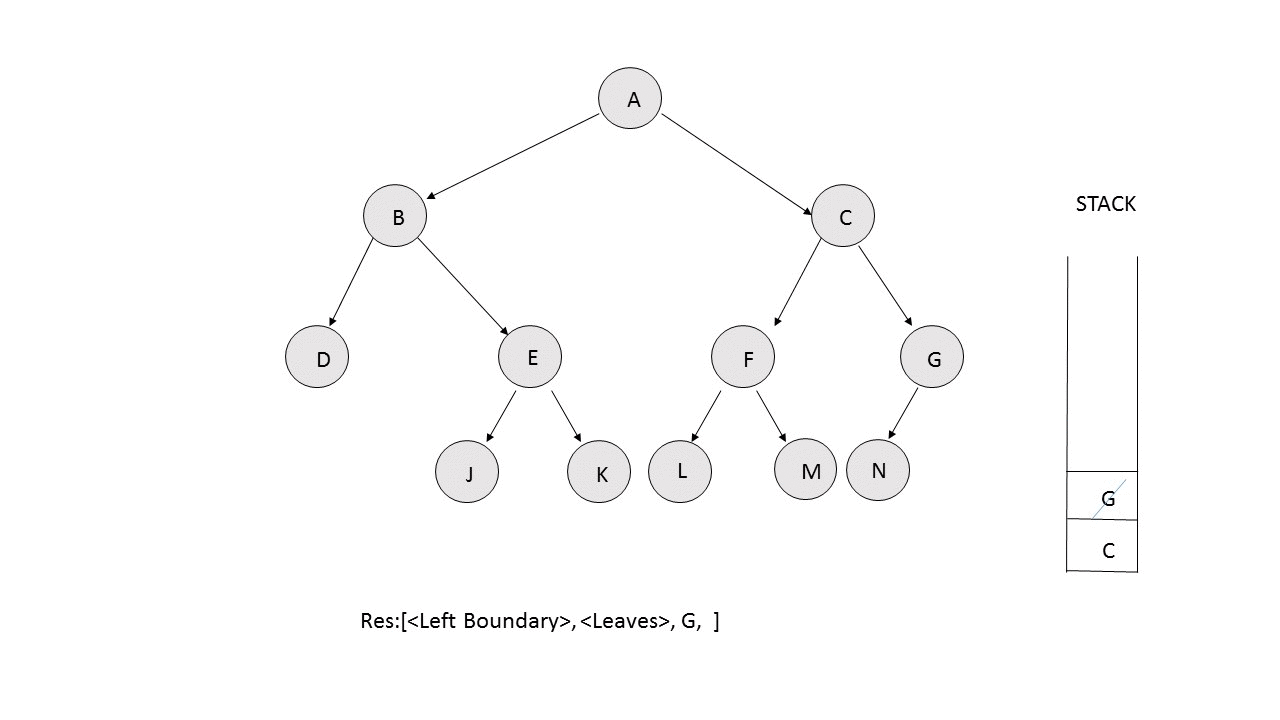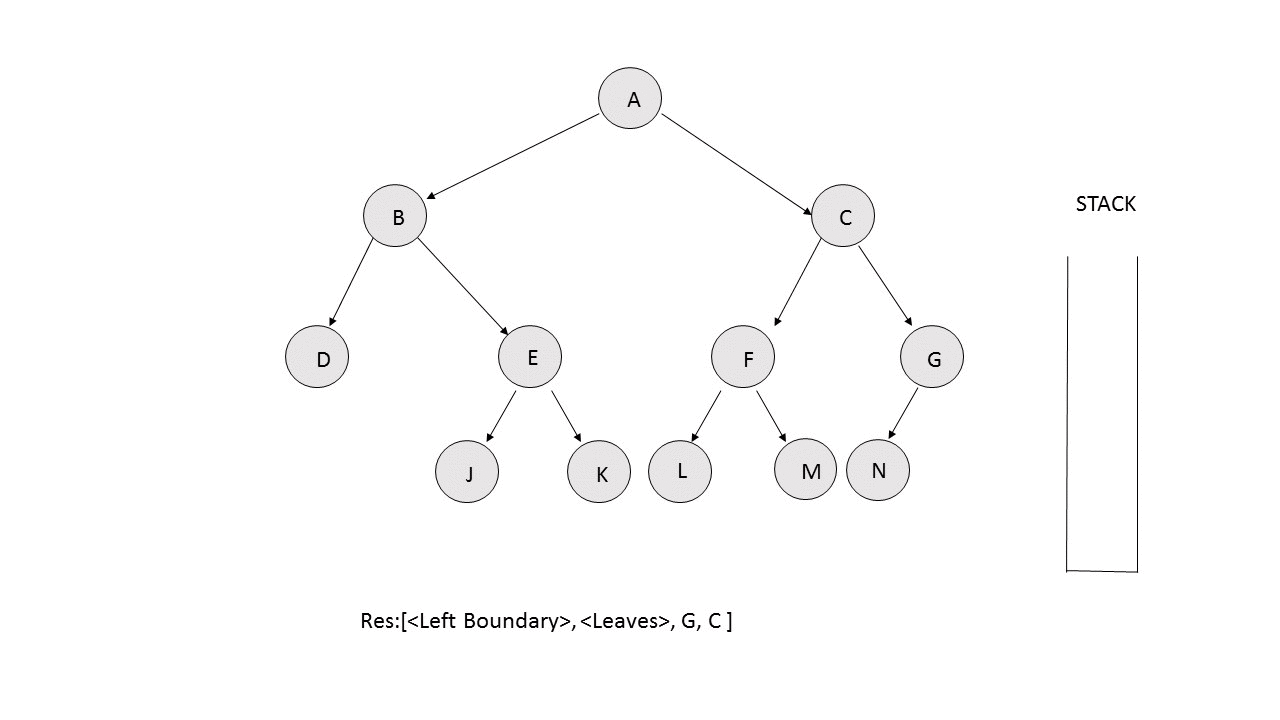
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
    bool isLeaf(TreeNode* root) {
        return !root->left && !root->right;
    }
    void addLeaves(TreeNode* root, vector<int>& res) {
        if (isLeaf(root)) {
            res.push_back(root->val);
            return;
        }
        if (root->left) addLeaves(root->left, res);
        if (root->right) addLeaves(root->right, res);
    }
public:
    vector<int> boundaryOfBinaryTree(TreeNode* root) {
        if (!root) return {};

        vector<int> res;
        if (!isLeaf(root)) res.push_back(root->val);
        // add left boundary
        TreeNode* cur = root->left;
        while (cur) {
            if (!isLeaf(cur)) res.push_back(cur->val);
            if (cur->left) cur = cur->left;
            else cur = cur->right;
        }
        // add leaf nodes
        addLeaves(root, res);

        cur = root->right;
        vector<int> tmp;
        // add right boundary
        while (cur) {
            if (!isLeaf(cur)) tmp.push_back(cur->val);
            if (cur->right) cur = cur->right;
            else cur = cur->left;
        }
        for (int i = tmp.size()-1; i >= 0; --i) {
            res.push_back(tmp[i]);
        }
        return res;
    }
};

Complexity Analysis

• Time complexity: $$O(n)$$ One complete traversal for leaves and two traversals upto depth of binary tree for left and right boundary.
• Space complexity: $$O(n)$$ $$res$$ and $$stack$$ is used.